Compute Shaders 2: Вычислительный блок

После первой статьи про вычислительные шейдеры меня попросили углубиться в аппаратную часть, чтобы охватить подгруппы и многое другое. Но прежде чем мы доберемся туда, давайте кратко опишем, как выглядит вычислительный блок (Compute Unit) и что происходит в нем.
В последнем посте я объяснил, что аппаратное обеспечение оптимизировано так, чтобы много элементов выполняли одну и ту же программу. Это привело к использованию очень широких SIMD-модулей (в случае GCN AMD ширина 16), сокрытию задержки памяти путем переключения задач и к модели ветвления, которая полагается на маскировку.
Исполнение на SIMD
Когда дело доходит до выполнения кода, вычислительный блок GCN имеет два основных строительных модуля, о которых надо знать: несколько SIMD и скалярный блок. Модули SIMD имеют ширину 16, значит, они обрабатывают 16 элементов за раз. Однако их латентность не равна латентности одного блока, т.е. они не заканчивают выполнение инструкции за один такт. Вместо этого для обработки команды от начала до конца требуется четыре такта (некоторые модули тратят больше времени, но давайте притворимся, что всегда четыре). Четыре такта — это скорость, которую вы ожидаете от чего-то вроде плавного умножения-сложения, которое должно получить три операнда из файла регистров, выполнить умножение и сложение и записать результат обратно (высоко оптимизированные CPU также тратят четыре такта, как это видно из таблиц Агнера Фога).
Но латентность не равна пропускной способности. При правильной конвейеризации команда с латентностью четыре может иметь пропускную способность один. Давайте посмотрим на пример:
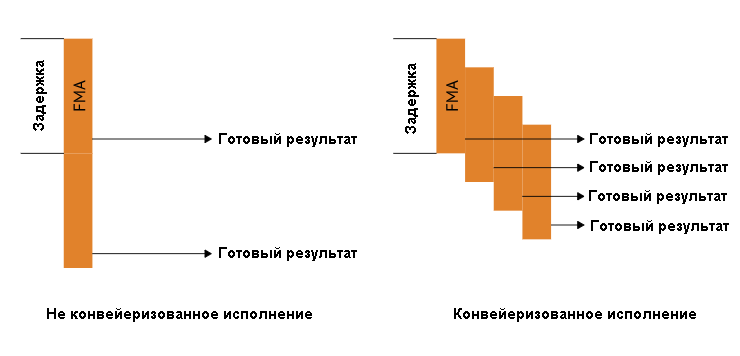
Сравнение конвейеризованного и не конвейеризованного блоков исполнения. Задержка четыре такта в обоих случаях, но после заполнения конвейеризованный блок имеет пропускную способность в одну команду за такт.
Это означает, что если у нас есть достаточно работы для одного SIMD, мы можем получить 16 выполненных команд FMA за такт. Но если бы мы выпускали разные команды в каждом такте, пришлось бы иметь дело с другой проблемой, когда некоторые из результатов не готовы. Представьте себе, что наша архитектура будет иметь задержку четыре такта для всех команд и рассылку в каждом такте (т.е. каждый такт мы можем вывести новую команду в конвейер). Теперь мы хотим выполнить этот воображаемый код:
v_add_f32 r0, r1, r2 v_mul_f32 r3, r0, r2
У нас есть зависимость между первой и второй командами — вторая не может начинаться до тех пор, пока не завершится первая, так как ей нужно ждать, пока не будет готов r0. Это означает, что нам пришлось бы приостанавливаться на три такта, прежде чем мы вышлем другую команду. Архитекторы GCN решили это, выпуская одну команду для SIMD каждые четыре такта. Кроме того, вместо выполнения одной операции на 16 элементах, а затем перехода на следующую команду, GCN выполняет одну и ту же команду четыре раза в общей сложности на 64 элементах. Единственное реальное изменение, которое это требует от аппаратного обеспечения, — сделать регистры шире, чем SIMD-модуль. Теперь вам не придется ждать, так как к моменту запуска v_mul_f32 на первых 16 элементах v_add_f32 только что закончил их:
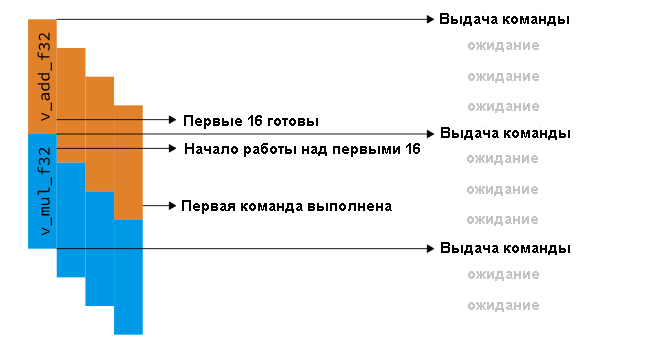
Выдача команды на единичном GCN SIMD. Команда выдается каждые четыре такта, и команды могут начинаться сразу одна за другой.
Вы сразу же заметите циклы ожидания, и это очевидно плохо, когда блок проводит в них большую часть времени. Чтобы заполнить ожидания, разработчики GCN используют четыре SIMD-модуля, поэтому реальная картина следующая:
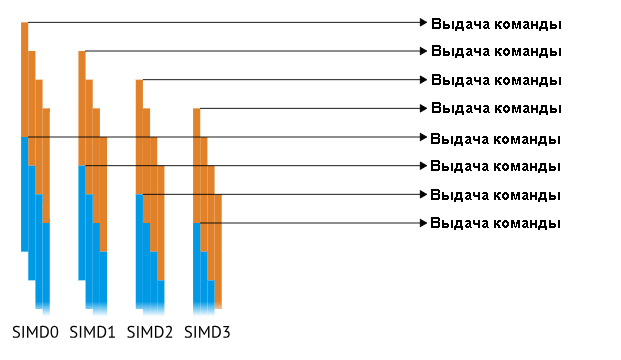
Путем дублирования SIMD четыре раза, одна команда может выдаваться каждый такт, что обеспечивает общую пропускную способность до 64 элементов / тактов (4 SIMD х 16 элементов / SIMD / тактов).
Эта конструкция в 64 элемента называется «вэйвфронт» или «вэйв» и является наименьшей единицей исполнения. Вэйв планируется на SIMD для выполнения, и каждая группа потоков состоит по крайней мере из одного вэйва.
Скалярный код
Фух, мы узнали уже довольно много, но до сих пор не достигли цели. Пока что мы притворяемся, будто все выполняется на SIMD, но помните: я писал, что с выполнением связаны два блока? Пришло время поговорить про второй.
Если вы программируете что-либо достаточно сложное, вы заметите, что существуют в действительности два вида переменных: равномерные, которые принимают постоянное значение для всех элементов, и неравномерные, которые отличаются в зависимости от полосы.
Неравномерной переменной может быть, например, laneId. Мы предполагаем, что есть специальный регистр для считывания g_laneId, а затем нужно выполнить следующий код:
if (laneId & 1) {
result += 2;
} else {
result *= 2;
}
В этом примере мы не будем говорить об условных переходах, потому что для них требуется компиляция ветки. Как бы это выглядело в GPU? Как мы узнали, есть штука, называемая маской исполнения, которая контролирует все активные полосы (она также известна как расходящийся поток управления). С учетом этого, вышеприведенный код будет скомпилирован, скорее всего, так:
v_and_u32 r0, g_laneId, 1 ; r0 = laneId & 1 v_cmp_eq_u32 exec, r0, 1 ; exec[lane] = r0[lane] == 1 v_add_f32 r1, r1, 2 ; r1 += 2 v_invert exec ; exec[i] = !exec[i] v_mul_f32 r1, r1, 2 ; r1 *= 2 v_reset exec ; exec[i] = 1
Какими на самом деле будут команды, не важно. Важно, что все рассматриваемые значения не совпадают в точности со значениями для полос. Т.е. для каждой отдельной полосы g_laneId имеет другое значение, нежели r1. Это “неравномерное” значение и одновременно случай по умолчанию, поскольку каждая полоса имеет в векторном регистре свой слот.
А теперь, если бы поток управления выглядел вот так, с приходящим из буфера констант cb:
if (cb == 1) {
result += 2
} else {
result *= 2;
}
Переводим это в прямой код:
v_cmp_eq_u32 exec, cb, 1 ; exec[i] = cb == 1 v_add_f32 r1, r1, 2 ; r1 += 2 v_invert exec ; exec[i] = !exec[i] v_mul_f32 r1, r1, 2 ; r1 *= 2 v_reset exec ; exec[i] = 1
Здесь внезапно возникает проблема, которой не было в предыдущем коде: cb является константой для всех полос, хотя мы и считаем, что нет. Раз cb является равномерным значением, сравнение с 1 можно было вычислить один раз, а не в каждой полосе. Так бы вы поступили в CPU, где векторные команды являются новинкой. Вы бы сделали обычный условный переход (повторяю, сейчас мы оставляем такие переходы за рамками внимания) и вызвали векторную инструкция для каждой ветки. Выходит, что GCN имеет схожую концепцию для “невекторного” исполнения кода, которое метко названо “скалярным”, поскольку вместо вектора он работает с одним скаляром. В конструкции GCN код может быть скомпилирован так:
s_cmp_eq_u32 cb, 1 ; scc = (cb == 1) s_cbranch_scc0 else ; jump to else if scc == 0 v_add_f32 r1, r1, 2 ; r1 += 2 s_branch end ; jump to end else: v_mul_f32 r1, r1, 2 ; r1 *= 2 end:
Что это нам дает? Большим преимуществом является то, что скалярные блоки и регистры супер дешевы по сравнению с векторными. В то время как векторный регистр имеет размер 64×32 бит, скалярный регистр составляет всего 32 бита. Поэтому мы можем накладывать на чип гораздо больше скалярных регистров, чем векторных. (По той же причине иногда бывают специальные регистры предикатов, в них по одному биту на полосу меньше, чем в полномасштабном векторном регистре.) Мы также можем добавить в скалярный блок экзотические инструкции по манипулированию битами, поскольку их не нужно повторять 64 раза за цикл. Наконец, мы используем меньшую мощность, поскольку скалярный блок перемещает и обрабатывает меньше данных.
Сведем все вместе
Теперь, когда вы можете назвать себя знатоком аппаратных средств, давайте посмотрим, как можно с пользой применить эти знания. Мы начнем с инструкций шириной вейвфронта, которые являются горячей темой для графических программистов. Ширина вейвфронта означает, что мы делаем что-то со всеми полосами, а не с одной. Что же именно мы делаем?
Скалярные оптимизации
Для начала, нам, наверно, надо поэкспериментировать с маской обработчика. В том или ином виде она присутствует в любом компьютерном оборудовании, иногда явно, а иногда как предикация. Соответственно, мы можем сделать аккуратную оптимизацию. Давайте рассмотрим следующий код:
if (distanceToCamera < 10) {
return sampleAllTerrainLayers ();
} else {
return samplePreblendedTerrain ();
}
Выглядит достаточно невинно, но обе функции обращаются к памяти сэмплов, и поэтому достаточно дороги. Как мы теперь знаем, при расходящемся потоке управления GPU будет выполнять оба пути. Даже хуже. Скорее всего, компилятор сформирует следующий псевдокод:
VectorRegisters<0..32> allLayerCache = loadAllTerrainLayers();
VectorRegisters<32..40> simpleCache = loadPreblendedTerrainLayers();
if (distanceToCamera < 10) {
blend (allLayerCache);
} else {
blend (sampleCache);
}
Проще говоря, он попытается максимально увеличить доступ к памяти. Поэтому к тому времени, когда мы достигнем пути else, есть приличная вероятность, что лимиты исчерпаны. Однако мы, как разработчики, знаем, что вариант со всеми слоями имеет более высокое качество. Поэтому как насчет такого подхода: если любая полоса идет по пути высокого качества, мы отправляем все полосы на этот путь. У нас будет чуть более высокое качество в целом, и кроме того, мы получим две оптимизации взамен:
- Не делая предварительной загрузки обоих вариантов, компилятор может использовать меньше регистров
- Компилятор может использовать скалярные ветки
На такой случай существует множество функций, все из которых работают с маской обработчика (или регистрами предикации, здесь и далее я буду считать их маской обработчика). Я буду говорить о следующих трех:
- ballot () — возвращает маску обработчика
- any () — возвращает exec != 0
- all () — возвращает ~exec == 0
Поменять код для такой цели очень просто:
if (any (distanceToCamera < 10)) {
return sampleAllTerrainLayers ();
} else {
return samplePreblendedTerrain ();
}
Еще одна распространенная оптимизация касается атомарности. Если мы хотим сделать инкремент глобальной атомарной переменной на единицу в каждой полосе, мы могли бы сделать это так:
atomic<int> globalAtomic;
if (someDynamicCondition) {
++globalAtomic;
}
Это потребует до 64 атомарных инкрементов в GCN (он не объединяет их на весь вейвфронт). Получается достаточно дорого, и мы могли бы поступить значительно лучше, если перевели код в такую форму:
atomic<int> globalAtomic;
var ballotResult = ballot (someDynamicCondition);
if (laneId == 0) {
globalAtomic += popcount (ballotResult);
}
Где popcount считает число установленных битов. Количество атомарных операций так уменьшается на 64. На самом деле, если вы делаете уплотнение, вам все равно понадобится иметь значения для каждой полосы. Этот случай настолько распространен, что у GCN, оказывается, есть для этого отдельная команда (v_mbcnt). Она автоматически используется компилятором для атомарных операций.
Наконец, еще кое-что про скалярный блок. Давайте предположим, что есть вершинный шейдер, который проходит через некий drawId, а пиксельный шейдер получает это как нормальный интерполянт. В таком случае (с запретом перекрестной оптимизации и оптимизации входной разметки вершин) вот такой код вызовет проблемы:
var materialProperties = materials [drawId];
Поскольку компилятор не знает, что drawId является однородным, он посчитает, что тот может быть неоднородным и сделает загрузку в векторные регистры. Если мы точно знаем, что он однороден — динамически однороден здесь конкретный термин — мы можем сообщить об этом компилятору. У GCN на такой случай имеется “стандартный” способ выражения — v_readfirstlane. Команда читает первую активную полосу и распространяет ее значение на все остальные. В архитектуре с отдельными скалярными регистрами это означает, что значение может быть загружено в скалярный регистр. Оптимальный код будет следующим:
var materialProperties = materials [readFirstLane (drawId)];
Теперь materialProperties хранятся в скалярных регистрах. Это уменьшает нагрузку на векторные регистры и превращает ветки, которые обращаются к свойствам, в скалярные.
Векторные забавы
Довольно про скалярный блок, давайте обратимся к векторному, потому что в нем все становится действительно интересным. Оказывается, пиксельные шейдеры оказывают огромное влияние на вычисления, потому что заставляют аппаратное обеспечение делать что-то невероятное — полосы начинают общаться друг с другом. До сих пор мы знали, что полосы не могут общаться иначе, как через LDS или трансляцией чего-нибудь через скалярные регистры (или считывания одной полосы). Но пиксельные шейдеры имеют очень уникальное требование — им нужны производные. Графические процессоры реализуют производные с использованием квадов, т.е. 2 × 2 пикселей, и обмениваются данными между ними динамически меняющимся образом. Мозг не взорвался?
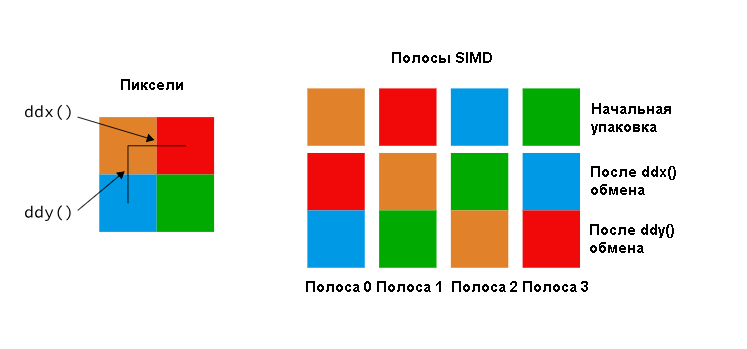
Пиксельные шейдеры могут обращаться к соседним полосам через команды ddx (), ddy (). Каждая полоса обрабатывает один пиксель, и в пределах 4 полос для обмена требуется брать много производных. С правой стороны мы можем видеть начальную упаковку и как производные тасуют данные между четырьмя полосами.
Это обычно называют свизлингом (quad swizzle). Редко какой графический процессор его не делает. Тем не менее, большинство графических процессоров идут намного дальше и обеспечивают больше, чем просто свизлинг на четырех дорожках. GCN идет намного дальше благодаря DPP — примитивов с параллельными данными. DPP обеспечивает поиск операндов в соседних полосах. Вместо перестановки участков в пределах одной полосы, функция позволяет одной полосе брать содержимое другой в качестве входных данных для команды, поэтому вы можете использовать выражение вроде такого:
v_add_f32 r1, r0, r0 row_shr:1
Что оно выполняет? Оно берет текущее значение в r0 на данной полосе и одно значение справа на том же SIMD (на нем установлен сдвиг по строкам вправо), суммирует их и сохраняет в текущей полосе. Это действительно серьезный функционал, который вводит новые состояния ожидания и имеет различные ограничения того, с какими полосами вы можете работать. Все это требует подробных знаний по реализации. Поскольку порядок обмена данных между полосами у разных производителей отличается, языки высокого уровня выставляют общие сокращения по всей ширине вейвфронта, наподобие min и т.д. Чтобы получить одно значение, проделывается либо свизлинг, либо DPP. С ними вы можете уменьшить значения в одном вейвфронте всего в несколько шагов, без доступа к памяти. Это быстрее и по-прежнему легко в применении — так почему оно не должно нравиться!?
Заключение
Надеюсь, к этому времени я смог пролить некоторый свет на реальную работу вещей. Осталось не так уж много из того, что я еще не упомянул. Для GCN это отдельные порты исполнения и обработка ожиданий. Об этом мы и поговорим в следующий раз.
