Геометрические шейдеры Unity

Ресурсов по шейдерам в Unity вообще достаточно мало. Но есть очень специфичный тип шейдеров, для которых ресурсов мало до странности (по крайней мере, на момент написания) — это геометрические шейдеры.
Я предполагаю, что люди не задумываются о них потому, что они могут быть неэффективными, а в некоторых случаях геометрические шейдеры можно заменить более быстрыми вычислительными. Тем не менее, они по-прежнему интересны для изучения, и с их помощью можно создавать действительно интересные эффекты.
Наиболее очевидный пример — это шейдеры для травы. В некоторых случаях генерация травинок или квадов с текстурой травы может быть лучше, чем создание повсюду травяных объектов. Плюс геометрические шейдеры могут дать больше гибкости, когда речь идет об оптимизации и настройке.
Я привожу здесь ссылки на некоторые тьюториалы и ресурсы, которые помогли мне понять геометрические шейдеры, поэтому определенно рекомендую их в качестве дополнительного материала:
- https://jayjingyuliu.wordpress.com/2018/01/24/unity3d-intro-to-geometry-shader/
- Шейдер травы в Unity – полный урок по созданию травы с помощью геометрических шейдеров
- Геометрические шейдеры на shaderslab.com
Предисловие
Прежде чем перейти к коду, давайте начнем с обзора того, что такое геометрический шейдер. Чтобы помочь мне проиллюстрировать их роль, представлю упрощенный конвейер рендеринга в реальном времени:
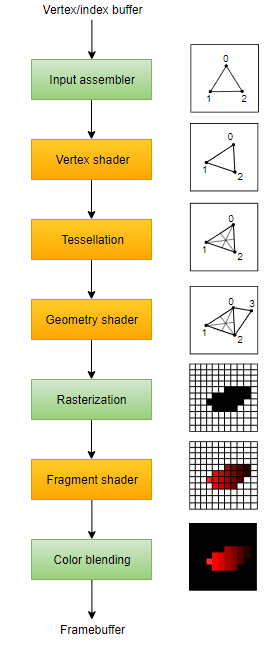
Рисунок взят из https://vulkan-tutorial.com/Drawing_a_triangle/Graphics_pipeline_basics/Introduction
Это про конвейер в Vulkan, но концепция очень похожа на другие конвейеры. Желтые прямоугольники — это фактические этапы конвейера, которые мы можем запрограммировать / переопределить с помощью шейдеров.
Основной вывод — геометрические шейдеры представляют собой шаг между вершинными и фрагментными, и эту концепцию вы будете замечать в примерах шейдеров. Их основная цель — получать информацию из отдельных вершин через вершинный шейдер, собирать примитивы, которые будут формировать объект (обычно это будут треугольники), и отправлять окончательную информацию на фрагментный шейдер для раскраски, освещения и т.д.
Однако самая крутая вещь в геометрических шейдерах, что когда они берут тройки вершин, образующих (например) треугольник, они могут не только определять, что происходит с этим треугольником, но также генерировать новые вершины и новые треугольники. Затем брать всю эту недавно сгенерированную геометрию и разворачивать ее, как делалось бы при смещении вершин в вершинном шейдере. Это позволяет, например, делать частицы из треугольников, как продемонстрировал VFX Mike.
Наконец, хотя их код поначалу может показаться пугающим, как только вы освоите некоторые вещи, использование шейдеров станет интуитивно понятным. И вы сможете лучше понять такие вещи, как UV и координаты пространства объектов. И, если вы чем-то похожи на меня, вы поймаете себя на том, что говорите: «О, чёрт, я не думал, что это сработает!».
Как писать геометрические шейдеры Unity
Я решил начать с простого геометрического шейдера без дополнительной функциональности, просто чтобы избавиться от писанины. Это также послужит аккуратным шаблоном для геометрических шейдеров, которые вы сами будете делать, поэтому на вашем месте я бы сохранил код где-нибудь неподалеку.
Давайте посмотрим на код:
Shader "Geometry/NewGeometryShader"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma geometry geom
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2g
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
};
struct g2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
v2g vert (appdata v)
{
v2g o;
o.vertex = v.vertex;
o.uv = v.uv;
return o;
}
[maxvertexcount(3)]
void geom(triangle v2g IN[3], inout TriangleStream triStream)
{
g2f o;
for(int i = 0; i < 3; i++)
{
o.vertex = UnityObjectToClipPos(IN[i].vertex);
UNITY_TRANSFER_FOG(o,o.vertex);
o.uv = TRANSFORM_TEX(IN[i].uv, _MainTex);
triStream.Append(o);
}
triStream.RestartStrip();
}
fixed4 frag (g2f i) : SV_Target
{
// sample the texture
fixed4 col = tex2D(_MainTex, i.uv);
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
ENDCG
}
}
}
ВАЖНО: Чтобы избежать любых неточностей, автор настоятельно рекомендует взять код из github. В частности, его WordPress не хотел правильно печатать «<», поэтому местами получалось «& lt;».
Прежде всего, мы должны сообщить общему шейдеру, что будем использовать геометрический шейдер. Поэтому нам нужно добавить еще одну инструкцию #pragma в строке 16, где мы говорим, что будет существовать метод, соответствующий геометрическому шейдеру, называемый «geom», который мы определим позже. Вот что делает «#pragma geometry geom», аналогично с вершинными и фрагментными шейдерами.
В данном случае мы не просто передаем данные из вершинного во фрагментный шейдер, у нас есть геометрический шейдер между ними. Поэтому нам потребуются три структуры данных вместо обычных двух:
- Структура «appdata», чтобы передавать свойства объекта в вершинный шейдер, как обычно.
- Структура «v2g», чтобы передавать данные из вершинного шейдера в геометрический.
- Структура «g2f», чтобы передавать данные из геометрического шейдера в фрагментный.
Сначала мы видим вершинный шейдер. Вместо объекта v2f теперь он возвращает объект v2g, который, как упоминалось выше, передает данные в геометрический шейдер. В этом простом случае вершина просто передает данные без каких-либо изменений.
В строке 48 я просто передаю позицию вершины в объектном пространстве как она есть, в строке 49 я делаю то же самое для координат UV вершины. Обратите внимание, что я не выполнял преобразование положения объекта в пространство отсечения и не использовал макрос «TRANSFORM_TEX» для UV, поскольку эти действия будут выполняться в геометрическом шейдере при передаче данных в фрагментный шейдер.
Имейте в виду, что на самом деле мы могли бы выполнить преобразование object-to-clip-position и вычисления UV в вершинном шейдере, и это может быть даже лучше, так как это будет сделано меньше раз. Но передача необработанных данных в геометрический шейдер дает нам больше гибкости в том, как мы обрабатываем их.
Геометрический шейдер в шаблоне кода
Здесь все сложнее. Первое, что вы сразу заметите, это совершенно другой синтаксис геометрического шейдера. Но мы пройдем его шаг за шагом.
В строке 53 над шейдером есть странный атрибут. Как следует из названия, «maxvertexcount» позволяет шейдеру знать максимальное количество вершин, которое будет добавляться данным геометрическим шейдером. Поскольку мы просто добавляем фактические треугольники объекта, будет выводиться 3 вершины.
Затем в строке 54 есть объявление метода, содержащее несколько странных параметров:
- triangle v2g IN[3] : Это массив из трех объектов v2g, каждый из которых соответствует одной вершине треугольника, который изучается в текущий момент. Тег «triangle» сообщает геометрическому шейдеру, что он будет ожидать треугольник в качестве входных данных. В качестве входных данных вы можете получить строку (поэтому понадобится массив объектов v2g размером 2) или точку (понадобится массив объектов v2g размера 1).
- inout TriangleStream<g2f> triStream : Если вы не заметили, то геометрический шейдер возвращает «void», поэтому на самом деле ни одного объекта, как это делал бы вершинный шейдер. Геометрический шейдер на самом деле добавляет каждый треугольник в список TriangleStream, который принимает объекты типа «g2f». Если вы хотите вывести линии, вы превратите их в «inout LineStream <g2f> lineStream», а если вы хотите вывести точки, это будет «inout PointStream <g2f> pointStream».
Теперь давайте перейдем к реальной функциональности. Геометрическому шейдеру нужно просто получить данные из вершинного шейдера и собрать треугольники, которые затем будут преобразованы во фрагменты и закрашены фрагментным шейдером.
Сначала в строке 56 мы создаем объект g2f, который будем использовать для постоянного изменения его полей, а затем добавляем объект в поток.
Затем мы сделаем простой цикл, чтобы добавить три входные вершины в поток и создать треугольник объекта. И поскольку эти данные поступают в фрагментный шейдер, я делаю все модификации, которые хочу, здесь.
Во-первых, в строке 60 я использую прием «UnityObjectToClipPos», чтобы преобразовать позицию входной вершины из объектного пространства в пространство отсечения. Затем макрос «UNITY_TRANSFER_FOG» для передачи всей информации о тумане Unity. В строке 62 я также использую макрос «TRANSFORM_TEX» для изменения UV-координат на основе информации о масштабировании и тайлинге «_MainTex». Все это делается для каждой из трех вершин треугольника так же, как делали бы в вершинном шейдере, если бы у нас не было геометрического.
Наконец, мы добавляем модифицированный объект «g2f» к потоку треугольников, используя «triStream.Append (o);». После цикла в строке 66 также есть прием «RestartStrip». Он должен сообщить потоку, что будет добавлять отдельный треугольник впоследствии. Здесь, поскольку мы не добавляем никаких новых треугольников, это на самом деле не нужно. Я добавил, чтобы вы могли легко скопировать код для последующей доработки.
Фрагментный шейдер в шаблоне
Наконец, в строках 69-76 у нас фрагментный шейдер. Вы можете заметить, что он совершенно не отличается от фрагментного шейдера по умолчанию в новом неосвещенном шейдере, за исключением того, что в качестве параметра он получает «g2f» вместо «v2f».
Выдавливание пирамид
Теперь у нас есть основа для геометрического шейдера, и мы можем создать на ней тот, который что-то делает. В частности, вот этот будет выдавливать пирамиды из каждого треугольника, просто добавляя точку в центре каждого и выдавливая пирамиду в направлении вектора нормали к плоскости.
Наглядный пример того, что мы будем делать с каждым треугольником:
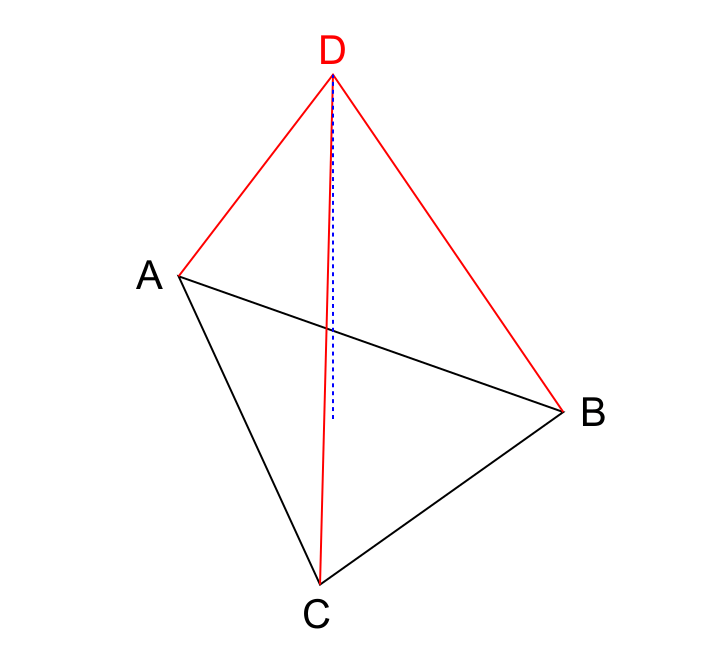
Посмотрим на код:
Shader "Geometry/TrianglePyramidExtrusion"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_ExtrusionFactor("Extrusion factor", float) = 0
}
SubShader
{
Tags { "RenderType"="Opaque" }
Cull Off
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma geometry geom
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
float3 normal : NORMAL;
};
struct v2g
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
float3 normal : NORMAL;
};
struct g2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
float4 color : COLOR;
};
sampler2D _MainTex;
float4 _MainTex_ST;
float _ExtrusionFactor;
v2g vert (appdata v)
{
v2g o;
o.vertex = v.vertex;
o.uv = v.uv;
o.normal = v.normal;
return o;
}
[maxvertexcount(12)]
void geom(triangle v2g IN[3], inout TriangleStream triStream)
{
g2f o;
float4 barycenter = (IN[0].vertex + IN[1].vertex + IN[2].vertex) / 3;
float3 normal = (IN[0].normal + IN[1].normal + IN[2].normal) / 3;
for(int i = 0; i < 3; i++) {
int next = (i + 1) % 3;
o.vertex = UnityObjectToClipPos(IN[i].vertex);
UNITY_TRANSFER_FOG(o,o.vertex);
o.uv = TRANSFORM_TEX(IN[i].uv, _MainTex);
o.color = fixed4(0.0, 0.0, 0.0, 1.0);
triStream.Append(o);
o.vertex = UnityObjectToClipPos(barycenter + float4(normal, 0.0) * _ExtrusionFactor);
UNITY_TRANSFER_FOG(o,o.vertex);
o.uv = TRANSFORM_TEX(IN[i].uv, _MainTex);
o.color = fixed4(1.0, 1.0, 1.0, 1.0);
triStream.Append(o);
o.vertex = UnityObjectToClipPos(IN[next].vertex);
UNITY_TRANSFER_FOG(o,o.vertex);
o.uv = TRANSFORM_TEX(IN[next].uv, _MainTex);
o.color = fixed4(0.0, 0.0, 0.0, 1.0);
triStream.Append(o);
triStream.RestartStrip();
}
for(int i = 0; i < 3; i++)
{
o.vertex = UnityObjectToClipPos(IN[i].vertex);
UNITY_TRANSFER_FOG(o,o.vertex);
o.uv = TRANSFORM_TEX(IN[i].uv, _MainTex);
o.color = fixed4(0.0, 0.0, 0.0, 1.0);
triStream.Append(o);
}
triStream.RestartStrip();
}
fixed4 frag (g2f i) : SV_Target
{
// sample the texture
fixed4 col = tex2D(_MainTex, i.uv) * i.color;
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
ENDCG
}
}
}
Перед геометрическим шейдером
Для этого шейдера я добавил новое свойство «_ExtrusionFactor», которое будет определять, насколько выдавленными будут пирамиды. Еще я добавил тег «Cull Off» в строке 11, чтобы избежать выбрасывания части граней из-за того, что некоторые треугольники нарисованы в неправильном порядке. На самом деле лучше было бы правильно нарисовать грани. Но давайте пока оставим так, чтобы легче использовать циклы.
Некоторые изменения были также сделаны в структурах данных. Чтобы получить вектор нормали каждой грани, сначала нужно получить вектор нормали каждой вершины, поэтому нам нужно добавить его как в структуры «appdata» и «v2g». Кроме того, в структуру «g2f» я добавляю поле цвета, которое поможет лучше визуализировать эффект.
Вершинный шейдер почти такой же, как и раньше, я просто передаю вектор нормали в данные «v2g» в качестве дополнительной информации.
Геометрический шейдер
Вот где на этот раз творится волшебство! Во-первых, вы можете заметить, что в строке 12 я упоминаю в качестве максимального количества для вывода в этом шейдере 12 вершин. Однако вы можете подумать, что это неправильно, поскольку мы добавляем только одну дополнительную вершину наверху пирамиды. По крайней мере, меня это изначально смутило. Но дело в том, что раз мы добавляем новые треугольники, нам придется добавлять каждую новую вершину, которая образует новый треугольник. Поэтому, поскольку мы добавим новый треугольник для каждого ребра, у нас будет 3 новых треугольника из 3 вершин в каждом, плюс исходный треугольник сетки с еще 3 вершинами. То есть 3 * 3 + 3 = 12 новых вершин. Видите, как это число может быстро выйти из-под контроля?
Для выдавливания нам понадобится центр каждого треугольника и вектор нормали к нему. Поэтому в строке 65 я вычисляю положение барицентра треугольника, получая среднее положение его точек, а в строке 66 получаю вектор нормали, также усредняя векторы нормалей каждой точки треугольника.
Затем я перехожу к созданию пирамид. Алгоритм выглядит так:
Для каждой из точек треугольника
- Получить индекс следующей точки
- Добавить вершину на месте текущей точки
- Добавить вершину в барицентре треугольника и вытянуть ее вдоль вектора нормали грани на величину, равную «_ExtrusionFactor»
- Добавить вершину на месте следующей точки
Именно это происходит в первом цикле for. В строке 69 я получаю индекс следующей точки, увеличивая i на единицу и используя модуль 3, чтобы не выходить за пределы диапазона массива. Затем в строках 71-75 я добавляю новую вершину точно так же, как в примере выше, только в этот раз я еще установил для нее значение цвета черным (в строке 74).
В строках 77-81 я делаю то же самое для точки пирамиды, но для ее положения я использую вычисленный барицентр, к которому добавляю вектор нормали, умноженный на «_ExtrusionAmount», чтобы переместить его вверх. Для кончика треугольника я использую белый цвет, так что выдавливание будет более очевидным.
Затем в строках 83-87 я делаю то же самое для следующей точки, также окрашивая ее в черный цвет.
Так как здесь мы фактически добавляем новый треугольник в каждый цикл, я добавил triStream.RestartStrip (); в конце цикла.
Наконец, после цикла в строках 92-99 я добавляю вершины исходного треугольника, также окрашивая его в черный цвет. И все готово:

Фрагментный шейдер
Фрагментный шейдер остается тем же самым, однако я умножаю цвет на «i.color», чтобы назначенные нами цвета вершин были видны.
Заключение
Надеюсь, это было достаточно нежное введение. Поначалу геометрические шейдеры Unity могут казаться пугающими, но после выяснения, почему они такие, какие есть, все становится намного яснее и определенно веселее. Я настоятельно рекомендую потренироваться с примерами из Shaderslab или с этими двумя шейдерами в посте, чтобы увидеть, чего вы можете достичь.
** Код в тьюториалах по шейдерам публикуется под лицензией CC0, поэтому вы можете свободно использовать его в своих коммерческих или некоммерческих проектах без указания авторства.
Источник: https://halisavakis.com/my-take-on-shaders-geometry-shaders/
